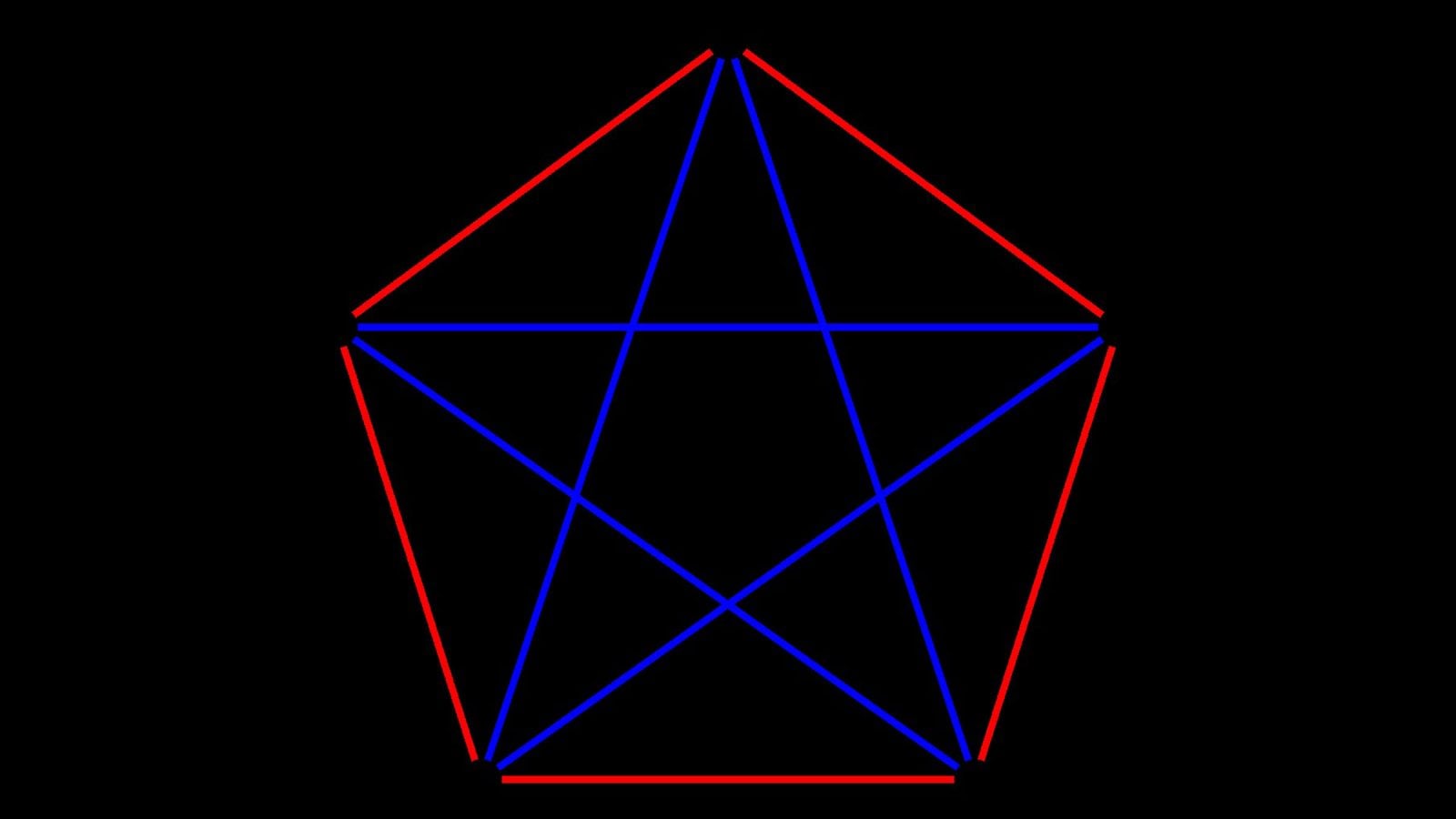
Twierdzenie Ramseya to twierdzenie matematyczne dotyczące teorii grafów, udowodnione przez Franka Ramseya. Jest ono banalnie proste, ale dość problematyczne pod względem matematycznym. Liczba Ramseya to minimalny rozmiar grupy potrzebny do zapewnienia, że pewna liczba punktów w tej grupie jest ze sobą połączona. Twierdzenie Ramseya najczęściej obrazuje się za pomocą metafory przyjęcia: ile osób trzeba zaprosić na dane przyjęcie, aby mieć pewność, że będzie na nim albo grupa trzech osób, które będą się znały, albo grupa trzech osób, które są zupełnie obce.
Czytaj też: To matematyka steruje biologią! Coraz bliżej odkrycia największej tajemnicy życia
Liczba Ramseya dla 3 to 6, a dla 4 to 18. Ile gości trzeba zaprosić na przyjęcie, by mieć pewność, że będzie wśród nich 5 gości lub nieznajomych? Wiadomo jedynie, że liczba ta mieści się między 43 a 48. Gdy liczby rosną, problem jest jeszcze poważniejszy, a liczby Ramseya trudniejsze do określenia. Więcej punktów to więcej możliwych połączeń, a także i więcej możliwych struktur dla samego grafu.
Prof. Marcelo Campos z Instituto Nacional de Matemática Pura e Aplicada (IMPA) w Brazylii mówi:
Jest tak wiele możliwości, że nie da się tego nawet brutalnie przeforsować.
Twierdzenie Ramseya dokładniejsze. To sztuka dla sztuki?
Matematycy mogą podać zakres dla każdej liczby Ramseya. W 1935 r. Paul Erdös doszedł do wniosku, że maksymalna liczba Ramseya dla danej liczby N to 4N. W 1947 r. opisał, że dolna granica to pierwiastek kwadratowy z 2N. Pomiędzy nimi znajduje się szeroki zakres liczb, a naukowcy od dekad robią wszystko, by go zawęzić.
Prof. Campos zrobił postęp w określeniu górnej granicy. Zamiast 4N, można teraz powiedzieć, że maksymalna liczba Ramseya dla danej grupy to 3,993N. Na pozór może się wydawać, że różnica nie jest duża, ale dla matematyków kolosalna. To pierwszy ważny krok naprzód w kwestii określenia górnej granicy liczb Ramseya od 1935 r.
Czytaj też: Nie radzisz sobie z matematyką? Winny może być poziom neuroprzekaźników w mózgu
Zespół prof. Camposa dokonał tego dzięki nowemu algorytmowi, który szuka pewnych podstruktur w wykresach węzłów. Szczegóły opisano w pracy opublikowanej na serwerze preprintów arXiv. Matematycy mają nadzieję, że górną granicę liczb Ramseya uda się doprecyzować, a być może kiedyś będzie możliwe stworzenie uniwersalnego wzoru.
Prof. Campos podsumował:
Nie sądzę, aby 3,99 było faktycznie punktem końcowym.
Więcej o teorii grafów i liczbach Ramseya od strony matematycznej można przeczytać na blogu DeltaMi.
